Permutation
In this lesson on Permutations, will learn more concepts on permutations and solve problems on them.
Recall n!
Without allowing things to repeat, n! permutations can be made taking all n different things at a time.
Without allowing any letter to repeat, 4 different letters can be arranged in 24 ways taking all at a time.
Now the next formula: npr
Definition of npr
Without allowing any letter to repeat, npr arrangements can be formed taking any r things out of n different things.
npr is the number of permutations
Without allowing any letter to repeat, 12 permutations can be formed taking any 2 out of 4 different things.
Consider four different letters a, b, c, d
Without allowing any letter to repeat, taking any 2 out of 4 different letters a, b, c, d, listed below are the
In npr, r signifies how many things each permutation should have.
In 4p2, each of 12 permutations must have 2, things.
Note:
If r = n, then
Solved Examples:
1. Find n if
np2=30
Solution:
So n = 6
2. Find r if
12p2=1320
Solution:
Therefore, r = 3
Definition of nr
Allowing things to repeat upto a maximum of r times, taking any r things at a time in each permutation, n different things can be arranged in nr ways
Useful Tip:
Use n! and npr to form permutations when things are not allowed to repeat.
Example:
Allowing things to repeat any number of times, arrange the three letters a, b, c
Without allowing things to repeat, listed below are the:
Allowing each thing to repeat (only 2 times here), listed below are more:

Allowing things to repeat any number of times, three different letters a, b and c can be arranged in 9 ways
Another example:
In how many ways 4 letters a, b, c, d can be arranged taking 3 at a time in each permutation?
Answer:
Include repetitions where there is scope and no restriction.
(Letters can repeat as there is scope and here repetitions are not prevented)
Using formula nr the number of permutations is 43 = 64
You will see three types of permutations in the 64 arrangements.
Type 1: When a letter repeats all three times. Eg: aaaSolved Examples
Type 2: When a letter repeats two times. Eg: aab
Type 3: When no letter repeats. Eg: abc
1. How many ways 5 prizes can be given away to 4 students, if each student can receive all the prizes?
Solution:Prizes are given away to students.
1st prize can be given away to any of 4 students in 4 ways;
Each of 2nd, 3rd, 4th and 5th prizes can be given away to all 4 students, as each of them can receive all prizes. So, each prize can be given away in 4 ways
5 prizes therefore can be given away in
2. How many numbers having 4 digits can be formed with non-zero even digits?
Solution:Non-zero even digits are: 2, 4, 6 and 8
Digits repeat in numbers and unless restricted, include repetitions.
Use nr.44 = 256 numbers having 4 digits each are formed.
Note: Here every three digit number is a permutation.
3. How many words having 5 distinct letters can be formed with the letters in the word MATHS?
Solution:
Unless restricted, letters normally repeat in words. [ like in add, dad]
But, the word “distinct” in the question restricts letters from repeating.
Recall n!
Without allowing things to repeat, taking all, n different things can be arranged in n! ways.
Here too, without allowing letters to repeat, taking all five letters from the word “MATHS”, 5! arrangements can be made.
The 120 arrangements or permutations are 120 words.
Let’s take up the next formula:

Note: In n! np2 and nr, we qualified the n things as n “different” things.
Its importance (why different) will get clear with the formula in hand now
How many ways you can
Only 6 ways. Listed below are the
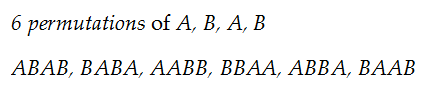
Why not more? Not possible!
Rearrange A with A and B with B in one sample permutation: AABB.
Look what happens! You get AABB. Oh, my! The same arrangement.
Got hold of why “different” was used to qualify n?
With four letters A, B, A, B in which 2 letters are identical and 2 other letters also are identical:
permutations can be made
Generalize. How? As follows:
The number of ways in which n things can be arranged taking all in each permutation, when p things are identical of one type and q things are identical of a second type is

Solved Examples:
1. How many words can be formed taking all the letters in the word “MISSISSIPPI”?
Solution:
Out of the 11 letters in the word:
4 are identical of one type (the 4 Is); 4 are identical of a second type (the 4Ss); and 2 are identical of a third type (the two Ps)
So,
arrangements can be formed.
Each arrangement is a permutation and a word too.
2. Six coins are tossed at a time. How many outcomes show 4 heads and 2 tails?
Solution:
Here, 4 Heads are identical of one type and 2 Tails are identical of a second type.
Apply

, and permutations are




