Surface area of a sphere.

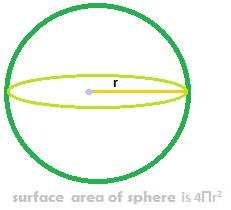
The total surface area of a sphere or simply the surfacea area of a sphere is 4Πr²

Solved Problems on surface area of a sphere

Example:

The surface area of a sphere is 2464 sq.cm s. Find the radius of the sphere.

Solution:

Surface area of a sphere is 4Πr²

So, 4Πr² = 2464, i.e.

4 × 22/7 × r² = 2464, so,

r² = (2464 × 7)/88 = 196

so, r = √196 = 14

so radius of the sphere is 14 cm's.

Example:

Find the percentage increase in the surface area of a sphere, if the radius of the sphere increases by 50%

Solution:

The surface area of a sphere is 4Πr²

After 50% increase in radius of the sphere, the new radius will become
(150/100)r  = 1.5r or 3r/2,

Substituting this in 4Πr², we get

4Π×(3r/2)² = 4Π (9r²/4) = (9/4)( 4Πr²)

So, the final surface area of a sphere, after its radius increases by 50%, will become
(9/4)( 4Πr²)

Now, the amount of increase in the surface area of sphere is:

(9/4)( 4Πr²) – (4Πr²) = (5/4)(4Πr²) = 1.25 × 4Πr²

Therefore, percentage increase in surface area of sphere is

(1.25 × 4Πr²) × 100%/( 4Πr²) =

1.25 × 100% = 125%

So, the surface area of a sphere increases by 125%, if the radius of the sphere increases by 50%