Interior angles are the angles that are formed between the sides of any polygon.

Exterior angle is the angle formed out of the figure.

Interior angles and Exterior angles:

Let us consider a point P on a straight line MR. Another line QP touches the point P and makes an angle of 30⁰ with PR. Hence, the angle QPR is the interior angle which makes 30⁰ and angle QPM makes angle 150⁰, which is called the exterior angle.

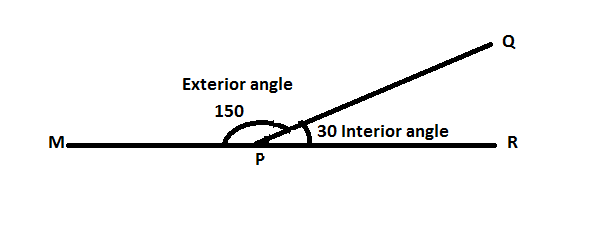
Note: For a straight line,

Interior angle + Exterior angle = 180⁰.

 Interior angless of Regular Polygons:

1. Triangle:

The angles formed between the sides of a triangle are interior angles.

As we know that the sum of all the three angles of a triangle is 180⁰.

In equilateral triangle, all the three angles measure same.

Hence the angle is 60⁰ in measure.

1. Quadrilateral:

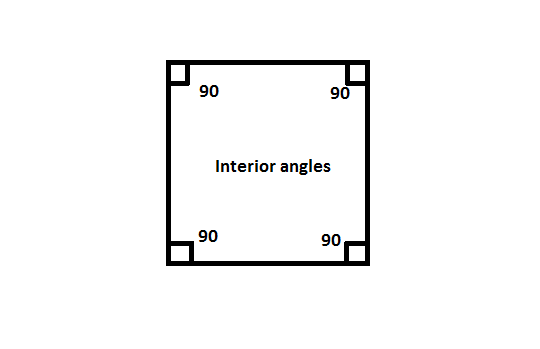
Plane figures which have four sides (like square, rectangle, etc.) are called quadrilaterals.

The interior angles of a regular quadrilateral is 90⁰ for each angle. Hence, the sum of interior angles is 360⁰.

1. Pentagon: In the five sided figure, pentagon, the interior angle is 108⁰, whereas the sum of the interior angles of all five sides is 540⁰.

Other polygons:

Following table gives the details of other polygons (from pentagon to nanogon).

If we observe as the number of sides is increased by one, 180⁰ is added to the sum of interior angles.

Explanation:

Pentagon has five sides and the sum of interior angles is 540⁰.

If the number of sides is increased by one, it becomes an hexagon with six sides and the sum of interior angles becomes 720⁰, (i.e. 540⁰ + 180⁰ = 720⁰.)

Hence, if another side is added then simultaneously 180⁰ is added to the sum of interior angles. Similarly, if side is removed then, 180⁰ is subtracted from sum of interior angles.

How to calculate the measure of each interior angle and also the sum of interior angles for any regular polygon?

It is simple to calculate the sum of interior angles and the measure of each interior angle if the number of sides of a regular polygon is given.

1. Sum of interior angle = (n-2)*180⁰

Or

Sum of interior angle = Interior angle * n

1. Interior angle = Sum of interior angles/n = ((n-2)*180⁰))/n

Where ‘n’ is number of sides.

Example:

Calculate the measure of each  interior angle and the sum of interior angles of a 10 sided figure.

Solution:

Given: Number of sides = n = 10

⇒Interior angle = ((10-2)*180⁰)/10

⇒Interior angle = 8*180⁰/10 = 144⁰

And, the sum of the interior angles = Interior angle * n = 144⁰ * 10 = 1440⁰

Supplementary angles

right angle.

straight angle.

Sign up today to receive Our Newsletter

Comment Box is loading comments...