Ratio and Proportion - Introduction

What you will learn in this lesson on Ratio and Proportion?

A ratio is comparison of two similar quantities.

For example, number 10 is twice as large as 5.

Now, a ratio can also be used to express this relation of

‘10 being double of 5’ as

10: 5, read as “10 is to 5”.

Also, the ratio 10: 5 can be written as a fraction 10/5 = 2

So, a ratio is a comparison tool.

In general, the ratio of a to b is written as



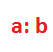
A ratio is a fraction.

The ratio a: b as a fraction is



In the ratio 10: 5, the two numbers 10 and 5 are called terms of the ratio.

Again, ratios are simplified.

Ratios are simplified by cancelling out common factors in the terms of the ratio.

Therefore, the ratio 10: 5 as a fraction is 10/5 = 2/1 = 2: 1.

So, 10: 5 = 2: 1 after canceling out the common factor 5.

A Ratio is not used to compare quantities of different units.

For example, the ratio of 5 yards to 5 meters is not 5: 5, i.e not 1: 1,

because yards and meters are not same units.

First, convert yards and meters into a same units: centimeters.

5 yards = 5 × 90 cms = 450 cms, and

5 meters = 5 × 100 cms = 500 cms.

So, the ratio of 5 yards to 5 meters is

450 cms: 500cms, i.e. 450: 500 = 9: 10

Now, if you wish to set off with your lesson on Ratio and Proportion in detail, then click on any of the links below:

Or, if you wish to capture a terse overview of each Ratio and Proportion formula, then go through each of the following header-links.

Or, you may as well click on the following header-links to take you to the page discussing in detail the specific Ratio and Proportion concept:

  • Ratios are always expressed in lowest terms.

4: 6 is simplified to 2: 3 by canceling out the common factor 2 from the terms of the ratio.

  • In a ratio, the order of the terms carries importance.

A father is 40 years old and his son 10 years.

The ratio of father’s age to his son’s age is 40: 10 = 4: 1

The father is 4 times as old as his son.

But the ratio 1: 4 signifies the ratio of the son’s age to that of the father.

In general, the ratio a: b is not the same as b: a, provided a ≠ b

  • Multiplying or dividing the terms of a ratio with a same number will not change the ratio.

a: b is same as m × a: m × b

for example, 2: 3 is same as 4 × 2: 4 × 3 = 2: 3

also, a: b is same as a/m: b/m

for example, 4: 6 which is 2: 3

is same as 4/2: 6/2 = 2: 3

  • How to compare ratios

Since ratios are fractions, comparing fractions will inherently compare ratios.

Which of the two ratios 4: 7 or 8: 12 is greater?

Answer: 4: 7 is 4/7 and 8: 12 = 2: 3 is 2/3

Now, is 4/7 > 2/3?

Find cross product to compare fractions

a/b < c/d, if a × d <  b × c

since, 4 × 3 < 7 × 2, therefore 4/7 < 2/3

  • How to divide a Whole Number into two parts whose ratio of division is given

Let $100 be divided between A and B in the ratio of 2: 3.

Then the share of A = [2/ (2+3)] × 100 = 40, and

Share of B = [3/ (2+3)] × 100 = 60, or

Alternatively, easily and common-sensically,

Share of B = 100 – 40 = 60

  • How to find A: B: C, if A: B and B: C are given?

Let A: B = 2: 3, and B: C = 4: 5, then

A: B: C = 8: 12: 15

Mnemonic to find A: B: C is


  • How to find A: B: C: D, if A: B and B: C and C: D are given?

Mnemonic to find A: B: C: D IS


Proportion

Proportion is equality of two ratios.

The ratio of 2 to 3 is same as the ratio of 4 to 6, i.e.

2: 3 = 4: 6

Therefore, the two ratios 2: 3 and 4: 6 are proportionate and written as:

2: 3:: 4: 6 and read as

The ratio of 2 to 3 is same as that of 4 to 6.

If 2: 3 = 4: 6, then

2 × 6 = 3 × 4, i.e. 12 = 12, i.e.

A Very important rule:

Let two ratios a: b and c: d be proportionate, i.e.

a: b :: c : d

(read as the ratio of a to b is same as that of c to d)

In the proportion a: b :: c : d

Product of means = product of extremes.

If a: b = c: d, then

a × d = b × c


There are two types of proportion.

They are Direct and Indirect proportion.

  • Direct proportion

If the ratio of a to b is same as the ratio of c to d, i.e. the ratios

a: b :: c: d, then a × d = b × c

Example:

if 3 pencils cost $30, then 5 pencils will cost what price?

Answer:

Set up a proportion as below:

3: 30:: 5: P, then 3 × p = 30 × 5, p = 50

  • Indirect proportion

If the ratio of a to b is inverse as the ratio of c to d, then

a: b:: d: c, then a × c = b × d

Example:

2 men finish a work in 3 days, then 3 men will do the same work in how many days?

Answer:

The ratio of 2 to 3 is indirect to the ratio of 3 to N, because more men take less days to finish a same work.

So, the ratio to be set up is like this:

The ratio of 2 to 3 is indirect to that of 3 to N, or

2 to 3 is same as that of N to 3.

So, 2: 3 :: N: 3, 2 × 3 = N × 3, i.e. N = 2.


Top
Next Lesson - Definitions in Ratios